11月2日は、東大寺学園高校の入試説明会がありました。
高校受験をする方の大半は公立中学校の生徒さんですが、その受験生に対して関西最難関男子校の1つである東大寺学園が求める能力が何であるかが気になったので、ひっそりと参加してきました。久しぶりに行きましたが、遠かったです。
高校の入試説明会の構成は、中学校の入試説明会と全く同じです。異なる点は、高校入試では公立高校が第一志望の生徒さんが多く、東大寺学園であっても「押さえ」の学校にする生徒さんが多いので、学校方針を含めた東大寺らしさを熱心にアピールされていたことくらいです。
中学校の進学説明会と同様に、科目ごとに先生が出題傾向や昨年度の問題の分析を説明されましたが、その中で数学の説明が中学受験にも通じる内容でしたので、ご紹介します。
まず、平成31年度東大寺学園高等学校・数学の入試問題の大問2をご覧ください。
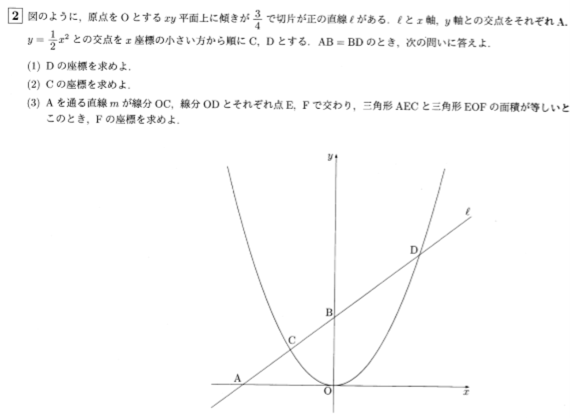
次に大問3をご覧ください。

■見慣れない形式の問題は正答率が低い
平成31年度の問題は大問が5つ出題されました。大問1は計算、大問2は二次関数、大問3は数の性質、大問4は平面図形、大問5は立体図形です。二次関数以外は、中学受験の出題傾向とほとんど同じです。同じ先生方が問題を作成されているので、当然と言えます。
大問2は最も正答率が高く、(1)と(2)は80%を超えています。一方で、大問3は(1)は76%ですが、(2)以降はそれぞれ、48.6%, 6.7%, 3.3%と極端に正答率が下がります。
大問3はとっつきにくい問われ方で、ぱっと見ただけで避けたくなるような問題ですが、じっくり見ると難しくありません。配布されたのは問題だけで解答がついてないために、100%の自信はありませんが、おそらく
(a-n)(b-n)を展開すると、ab-na-nb+n2となり、これを(条件)の式に代入することで、
(a-n)(b-n)=4n2となるのかな、と説明会会場でカリカリ解いていました。間違っていましたら、コメントで教えてください。こっそり修正します。
(2)はn=2であれば、数が小さいので1つずつ数えることで解くことができます。
■パターン学習だけでは限界がある
問題文で数学独特の表現で書かれると難しく感じますが、「展開してみる」ことに気づけば簡単です。
大問3の出題意図は「見たことのない問題が出題された時、どうやって解けばいいか、諦めないでさまざまな方法で取り組んでみてほしい」と説明されました。
大問2のような塾や問題集で頻出パターンである問題は、見ただけで解法がすぐに分かるために簡単に解くことができますが、大問3のような見たことのない問題は、パターン学習では対応できません。したがって、どこから手をつけていいか分からなくなる生徒さんが出てきます。
パターン学習はある程度の効果はありますが、一方で限界もあります。見たことのない出題形式の問題が出るたびにすべてパターンとして覚えることはできません。
■すぐに諦めないで複数の解き方を見つけられるか
自分が見たことのない問題に直面した時に、「出来ない」「分からない」とすぐに諦めるのではなく、まずは、思いつく何通りかのやり方で解いてみてほしい。そのようなアプローチのできる生徒さんを学校は求めているとのことでした。
大問3は灘中の1日目で出題されそうな問題です。平方根は中学校課程の内容なので、全く同じ問題は出題されませんが、数の性質をうまく使って、式を13や7などの素数で括りなおすやり方を知っていれば、大問3の(1)は簡単です。
(2)で1つずつ数字を入れながら何通りあるかを考えるうちに、この問題の規則性を見つけて、(3)と(4)を解いてほしいという出題者側の意図があるようです。
■未知の問題に持てる知識の総動員で挑めるか
東大寺学園高等学校の進学説明会でのお話と全く同じことを、算数の補講塾でも言われました。
1問5分の持ち時間として、最初の30秒くらいで持てる全ての知識を総動員して、解き方を考えてみる。解き方が多く浮かぶようになってほしい。1つ目の解き方で解答までたどり着けない時は、次の解き方で解いてみる。
文章で書くと長い時間をかけてるように伝わるかもしれませんが、本番の入試では、解き方の道筋を見つけるまでを2分ほどでやらなければなりません。
灘、甲陽、東大寺の算数は別格です。
短時間で、粘り強く、複数の解き方が浮かんで、その中で最も可能性の高い方法でぱっと解いてみる。
求められる能力が高すぎます。
■過去問は学校からのメッセージ
パターン学習はある程度は有効です。昨日の進学説明会でも「過去問は学校からのメッセージです」との言葉は何度も繰り返されました。まずは、過去問で出題傾向を確認することです。
算数の過去問解きの際は、パターン問題であるか、問われ方がひねられているかにまず注目し、ひねられた問題に対して何通りの解き方が浮かぶかを確認されてみてください。
本当は、複数通りの解き方を思いつくような粘り強い挑み方は、5年生までで特訓することが理想です。保護者様が指導するのはなかなか難しいですが、超難問対策はこのやり方がいちばん効果的だと思います。








コメント